Pomůcka DEMONSTRAČNÍ KARTY pro výuku násobilky je dodávána jako archy, které je zapotřebí rozstříhat na kartičky. Jednotlivé kartičky je možné podlepit malými magnety, a usnadnit tak žákům manipulaci s nimi na magnetické tabuli.
OBSAH SOUBORU
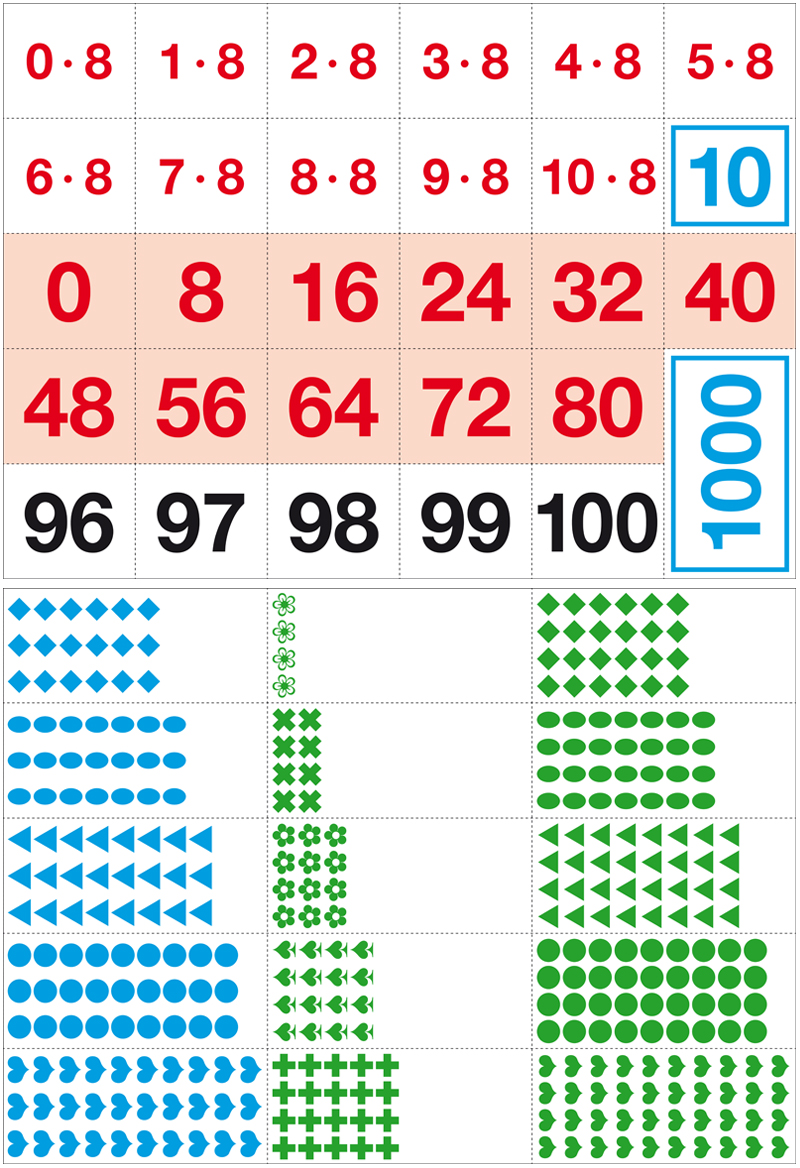
- Karty se znázorněním násobilkových spojů. (Na kartách jsou stejné tvary, jako mají žác
 i na kartonových přílohách v Matematice ALTER, sešity č. 6 a 7.)
i na kartonových přílohách v Matematice ALTER, sešity č. 6 a 7.) - Ke každé násobilce jsou na kartičkách všechny dvojice činitelů a všechny násobky. Vše je ve stejných barvách jako na kartonových přílohách v sešitech.
- Prázdná karta pro znázornění násobilkových spojů s nulou je v souboru pouze jedna.
- Kartičky s čísly 0 až 100
- Jedenáct kartiček s desítkou
- Deset kartiček se stovkou (pro 3. ročník)
- Jedna kartička s tisícem (pro 3. ročník)
-
Využití pro numeraci do sta
-
HRA NA ZTRACENÁ ČÍSLA
- Vyučující (nebo sami žáci) srovná na magnetickou tabuli čísla po desítkách od nuly do sta. V každé desítce obrátí několik kartiček číslem dospodu. Žáci doplňují chybějící čísla a říkají, např.: „Ve druhé desítce doplníme čísla 14, 17, 19.“ Obrácením kartičky zkontrolují, zda doplnili správná čísla.
- Postup je podobný, jenomže kartičky s čísly sejmeme z magnetické tabule. Každý žák si vybere tři kartičky bez ohledu na to, ze které desítky vybraná čísla jsou, a zařadí je na správné místo.
- Pomocí těchto kartiček můžeme procvičovat vztahy „před“, „za“, „hned před“, „hned za“.
HRA NA BRANKÁŘE
- Vyučující si ponechá z každé desítky jednu kartičku. Ostatní kartičky rozdá žákům. Ti si rozloží kartičky na lavici. Vyučující ukáže číslo a vyzve žáky, aby přinesli kartičky s menšími (většími) čísly. Žáci nemusí rovnat čísla do desítek. Připevní číslo neuspořádaně na magnetickou tabuli a odůvodní: „Přinesl/a jsem číslo 27, protože je menší než číslo 42.“ Mohou také říct proč: „Číslo 27 je menší než 42, protože má menší počet desítek.“ (Při stejném počtu desítek porovnají žáci počet jednotek. Číslo 51 má stejný počet desítek jako číslo 56, má však menší počet jednotek. Číslo 51 je tedy menší než číslo 56.) Bystří počtáři mohou říct i opačný výrok: „Jestliže je číslo 27 menší než číslo 42, pak můžeme také říct, že číslo 42 je větší než číslo 27.“
- Zadání můžeme vymezit, např.: „Přineste čísla větší než 35 a menší než 50.“
- Procvičujeme pojmy první, druhá, ... desátá desítka, např.: „Vyber dvě čísla ze sedmé desítky.“ Tato vybraná čísla nechávají žáci neuspořádaně v dolní části magnetické tabule a komentují: „Ze sedmé desítky jsem vybral/a čísla 62 a 68.“
- Po skončení práce podle 3. odstavce mohou další žáci zase vkládat vybraná čísla na jejich původní místo s odůvodněním, např.: „Mezi čísly 75 a 77 leží číslo 76. Číslo 76 je větší než 75 a menší než 77.“
-
Numerace do tisíce (3. ročník)
-
Karty se znázorněním tisíce, stovek, desítek a kolečka, která představují jednotky, můžeme použít ke znázorňování čísel do tisíce.
Např.: 648
Na takovém znázornění žáci dobře pochopí i rozvoj čísla v desítkové soustavě:
648 = 6 · 100 + 4 · 10 + 8 · 1 -
Násobení a dělení v oboru malé násobilky
-
1. ŘADY ČÍSEL
Na magnetické tabuli sestavíme řadu čísel do 20 (30, 40 ...). Násobky dané násobilky (černá čísla) žáci zamění za barevné kartičky násobků. Tak získají názornou představu o poloze násobků v řadě čísel.
2. TVORBA SLOVNÍCH ÚLOH
Kartičky se znázorněním, s dvojicemi činitelů a násobky dobře poslouží při vyvozování jednotlivých násobilek a dělení. Používáním kartiček se znázorněním motivujeme žáky k tvoření slovních úloh, např.:
a) Za jednu minutu vyrobí stroj __ vykrajovátek ve tvaru lístečku. Kolik takových vykrajovátek vyrobí stroj za 2, 3, ... 10 minut?
b) V bonboniéře byla čokoládová srdíčka. V jedné řadě bylo __ srdíček. Kolik srdíček bylo ve 2, 5, 8, 10 takových řadách?
c) Hračky byly srovnány v krabičkách takto:
1. krabička – 7krát 2 balónky
2. krabička – 4krát 3 kytičky
3. krabička – 9krát 4 kostky ze stavebnice ... apod.
Kolik hraček je v jednotlivých krabičkách?
Více podobných úloh např. o hračkách či o obrázcích vymyslí jistě i sami žáci.3. VYVOZENÍ NÁSOBILKY
Na magnetickou tabuli připravíme kartičky se znázorněním. Pod každou z nich položíme kartičku s dvojicí činitelů a s příslušným násobkem. Velkou předností tohoto způsobu vyvozování násobilek je propojení vytvářených násobilkových spojů s názornou představou.
Z této sestavy žáci vyvozují jednotlivé příklady násobilky. Žáci s kartami pracují tak, že rozdané karty doplňují na příslušná místa na magnetické tabuli. Až po nacvičení práce s těmito demonstračními kartami přecházíme ke kartičkám, které má každý žák. Vyučující říká různé příklady z nacvičované násobilky, žáci je ukazují v řadě a počítají. Velmi brzy se tak naučí orientaci v sestavených řadách a snadno příklady vyhledávají i řeší. Při nácviku by měl žák vnímat každý příklad jako zobrazení a řešení určitých konkrétních situací. Je velmi účinné hned od počátku nechat žáky k daným příkladům tvořit slovní úlohy, v nichž mají z počtu stejných částí a velikosti jedné z nich určit celek.4. VYVOZENÍ DĚLENÍ
Z výše uvedené sestavy kartiček můžeme vyvozovat i příklady na dělení. Násobky se stanou dělencem, jeden z činitelů dělitelem a druhý podílem. To, že žáci vidí i znázornění příkladu, usnadňuje zapamatování těchto spojů.
Při nácviku dělení žáci zpočátku určují z celku a velikosti jedné části počet částí (např. rozdělujeme po dvou, po třech ...). Tento způsob je snazší pro žáky, mají-li sami provést znázornění.
Později se učí výpočtem určovat z celku a počtu stejných částí velikost jedné z nich (počítáme např. polovinu, třetinu ...).Nedílnou součástí nácviku dělení je i tvoření slovních úloh. Ty budou opět spojeny s vnímáním konkrétních vyobrazení, např.:
a) V cukrárně rovnali koláče v krabicích do řad po třech. Do kolika řad srovnali 12 koláčů?
b) 12 koláčů rozdělila paní cukrářka do třech řad. Kolik koláčů bylo v každé řadě?5. PROCVIČOVÁNÍ NÁSOBENÍ A DĚLENÍ
Pracujeme s demonstračními kartami a všichni žáci pracují současně s vlastními kartičkami.
a) Ke kartičkám s násobky žáci přiřadí kartičky s dvojicemi činitelů. (Násobky mohou být v uspořádané nebo neuspořádané řadě.)
b) Ke kartičkám se znázorněním žáci vytvoří jeden nebo dva příklady na násobení a jeden nebo dva příklady na dělení.
c) Žáci dokáží hbitě srovnat vzestupné i sestupné řady násobků.
d) Žák ukáže kartičku s násobkem a ostatní vyhledají správnou dvojici činitelů, která k danému násobku patří.
e) Žák ukáže kartičku s dvojicí činitelů, ostatní vyhledají kartičku se znázorněním daného příkladu.
f) Žák ukáže kartičku se znázorněním a ostatní vyhledají příslušnou dvojici činitelů a násobek, který odpovídá součinu těchto činitelů.
g) Žák ukáže kartičku se znázorněním, ostatní se k němu pokusí vytvořit slovní úlohu.
h) Na kartičce se znázorněním žáci ukazují polovinu, třetinu, čtvrtinu, pětinu atd.
R: Žáci s hlubším zájmem o matematiku mohou ukazovat i dvě třetiny; dvě, tři čtvrtiny; dvě, tři, čtyři pětiny atd.6. VYHLEDÁVÁNÍ NEJBLÍŽE MENŠÍHO NÁSOBKU (příprava na dělení se zbytkem)
Pro toto cvičení si sestavíme řadu všech čísel v oboru nacvičované násobilky. Násobky vyznačíme barevnými kartičkami. Pak vybíráme nejblíže menší násobky nacvičované násobilky ke všem číslům, která jsou vytištěna černě, např.:
Nejblíže menší násobek tří k číslu
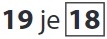
Nejblíže menší násobek tří k číslu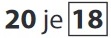
Podobně můžeme postupovat ve třetím ročníku při nácviku dělení se zbytkem.